Using Ray Casting Algorithm to determine if a point inside a polygon

,

Approach Overview

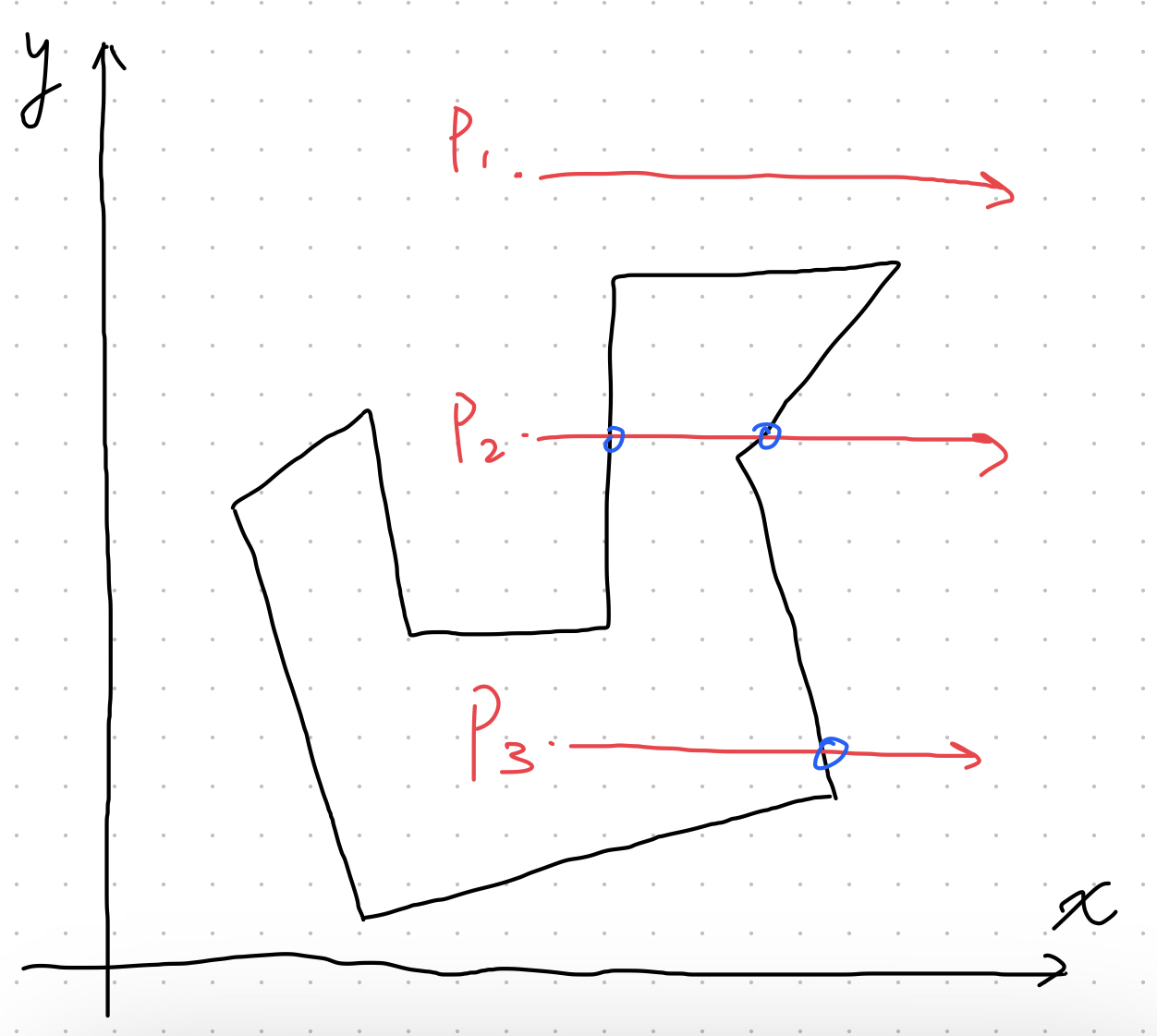
The figure illustrates the functioning of the Ray Casting Algorithm in determining whether a point lies within a polygon.

To determine if the point lies within the polygon, simply create a ray extending from the given point in any direction. Then, count the total number of intersections between the ray and the polygon boundary. If it is odd, the point is inside the polygon.

In this way, as the figure illustrate:

  • The ray starting from P1 does not intersect with the polygon boundary, indicating that P1 is located outside the polygon.

  • The ray originating from P2 intersects the boundary twice, yielding an even count, which indicates that P2 is situated outside the polygon.

  • Conversely, the ray originating from P3 intersects the boundary only once, resulting in an odd count, indicating that P3 lies inside the polygon.

Figure 1

Code

Here is a piece of Python code script to implement this approach.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# coding: utf-8
from enum import Enum


# use enum to define the relation
class Relation(Enum):
    WITHIN = 1
    BOUNDARY = 2
    OUTSIDE = 3


# use list such as [x, y] to represent a point
# use list such as [ [x0, y0], [x1, y1], [x2, y2] ... [xn, yn] ] to represent a 2D polygon without inner holes
# [x0, y0] is the same as [xn, yn], which means the polygon is closed.
def check_in_poly(point, polygon):
    # variable intersection_num indicates the counter of the num of points that the ray intersect with the polygon
    intersection_num = 0

    px, py = point[0], point[1]
    # The ray direction is along the X-axis direction
    for i in range(len(polygon)):
        # v1, v2 are vertex of the polygon,
        v1 = polygon[i]
        v2 = polygon[i + 1]
        v1x, v1y = v1[0], v1[1]
        v2x, v2y = v2[0], v2[1]

        # check if point overlap with a vertex point
        if px == v1[0] and py == v2[0]:
            return Relation.BOUNDARY

        # check if the ray go through the edge{v1, v2}
        if py > max(v1y, v2y) or py < min(v1y, v2y):
            # won't intersect with this edge
            continue

        if v2y != v1y:
            x_expect_on_line = (py - v1y) * (v2x - v1x) / (v2y - v1y) + px
            if px == x_expect_on_line:
                return Relation.BOUNDARY
            elif px < x_expect_on_line:
                intersection_num += 1

        return Relation.WITHIN if intersection_num % 2 == 1 else Relation.OUTSIDE

Reference:

  1. Ray Casting Algorithm